Numpy character embeddings

(Continues from Embedding derivative derivation.) Let’s implement the embedding model in numpy, train it on some characters, generate some text, and plot two of the components over time.

Vec transpose

To implement the derivative we need the vec-transpose operator. Numpy doesn’t have an implementation but we can implement our own by doing some reshaping and transposition:

def vec_transpose(X, p):
    m, n = X.shape
    return X.reshape(m / p, p, n).T.reshape((n * p), m / p)

Commutation matrix

There is an implementation of the construction of the commutation matrix in statsmodels.tsa.tsatools that we can use.

def commutation_matrix(p, q):
    K = np.eye(p * q)
    indices = np.arange(p * q).reshape((p, q), order='F')
    return K.take(indices.ravel(), axis=0)

Objective function

A straightforward implementation of the log likelihood and log likelihood derivatives (using the previous notation) for a single data point in python yields:

def log_likelihood(x, sample_weight, W, R, C):
    logZ = -np.inf
    p = 0.0
    for c in range(C):
        en = np.dot(np.dot(x, R), W[c])
        logZ = np.logaddexp(logZ, en)
        p += en * y[c]
    ll += (p - logZ) * sample_weight

def dlog_likelihood(x, sample_weight, W, R, C):
    dlldW = [np.zeros(Wc.shape) for Wc in W]
    dlldE = np.zeros(E.shape)
    
    for c in range(C):
        en = np.dot(np.dot(x, R), W[c])
        dlldW[c] += (np.dot(np.dot(y[c], x), R) - np.exp(-logZ + en) \
                    * np.dot(x, R)).reshape(dlldW[c].shape) \
                    * sample_weight
        
        inner = np.dot(np.dot(W[c], x.reshape(1, -1)), K_mv).T
        term = np.dot(K_hm_m_T, vec_transpose(inner, M)).T
        dlldE += ((y[c] - np.exp(-logZ + en)) * term) * sample_weight

Now the total log likelihood is calculated as:

def objective(params, (M, H, X, Y, sample_weights)):
    V = X.shape[1] / M
    N, C = Y.shape
    E = params[0: V * H].reshape(V, H)
    W = [params[V * H + c * M * H: V * H + (c + 1) * M * H].reshape(M * H, 1) 
         for c in range(C)]
    R = np.kron(np.eye(M), E)
    
    K_hm_m_T = vec_transpose(commutation_matrix(H, M), M).T
    K_mv = commutation_matrix(M, V)
    
    ll = 0.0
    dlldW = [np.zeros(Wc.shape) for Wc in W]
    dlldE = np.zeros(E.shape)
    
    for x, y, sample_weight in zip(X, Y, sample_weights):
        ll += log_likelihood(x, sample_weight, W, R, C)
        dlldW_delta, dlldE_delta = dlog_likelihood(x,
                                                   sample_weight,
                                                   W, R, C,
                                                   K_hm_m_T, K_mv)
        for c in range(C):
            dlldW[c] += dlldW_delta[c]   
        dlldE += dlldE_delta

    dparams = np.concatenate([d.flatten() for d in [dlldE] + dlldW])
    return -ll, -dparams.T

Character N-grams

To construct the training data the input string is first split into N-grams (in our case M-grams), and then counted. This reduces the number of training points, and hence the training time.

text = open('input.txt', 'r').read()
vocab = list(set(text))
V = len(vocab)
vocab_to_index = {v: i for i, v in enumerate(vocab)}

ngrams = {}
M = 3
for i in xrange(len(text) - (M + 1)):
    ngram = text[i: i + (M + 1)]
    ngrams[ngram] = ngrams.get(ngram, 0) + 1
N = len(ngrams)

We then sort the points M-grams from most common to least common (because curriculum learning, or something), and construct the input feature vectors.

scounts = sorted(ngrams.items(), key=lambda x: -x[1])
scounts[:10]

train_x = np.zeros((N, V * M))
train_y = np.zeros((N, V))
for n, (ngram, _) in enumerate(scounts):
    init = ngram[:-1]
    y = ngram[-1]
    for i, token in enumerate(init):
        train_x[n, i*V + vocab_to_index[token]] = 1
    train_y[n, vocab_to_index[y]] = 1
train_sw = [count for _, count in scounts]

(I’m not bothering with train/test splits because this implementation is too slow to take seriously)

Training

Now we decide on our embedding size—in our case 5—and get an initial random parameter vector.

H = 5
x0 = random_params(M, H, V, V, std=1.0 / M)

I’ve wanted to check out Jascha Sohl-Dickstein’s minibatch version of the BFGS optimizer for a while and it was fairly easy to plug the objective into that.

from sfo import SFO

minibatch_size = 400
subs = [(M, H,
         train_x[n * minibatch_size: (n + 1) * minibatch_size].copy(),
         train_y[n * minibatch_size: (n + 1) * minibatch_size].copy(),
         train_sw[n * minibatch_size: (n + 1) * minibatch_size],
         ) for n in range(len(train_sw) / minibatch_size)]
optimizer = SFO(objective,
                x0.copy(),
                subs,
                max_history_terms=6,
                hessian_algorithm='bfgs')

Embedding evolution

To make a gif of how the character embeddings evolve during training we’ll need to save the intermediate parameter vectors.

Also the first optimizer step must be two steps for some reason.

param_list = []
param_list.append(optimizer.optimize(num_steps=2).copy())
for step in range(500):
    param_list.append(optimizer.optimize(num_steps=1).copy())

Make a gif

Using this recipe, the first two components (out of the possible 5) is plotted over time.

from matplotlib import animation

frame_factor = 2
def animate(nframe):
    plt.cla()
    E = param_list[nframe * frame_factor][0: V * H].reshape(V, H)
    for i, char in enumerate(vocab):
        plt.text(E[i, 0], E[i, 1], char)
    plt.scatter(E[i, 0], E[i, 1], marker='.')
    plt.ylim(-1.1, 1.5)
    plt.xlim(-2.5, 1.1)
    plt.title('Iteration {}'.format(nframe))

fig = plt.figure(figsize=(12, 12))
anim = animation.FuncAnimation(fig, animate,
                               frames=len(param_list) / frame_factor)
anim.save('embeddings.gif', writer='imagemagick', fps=32);

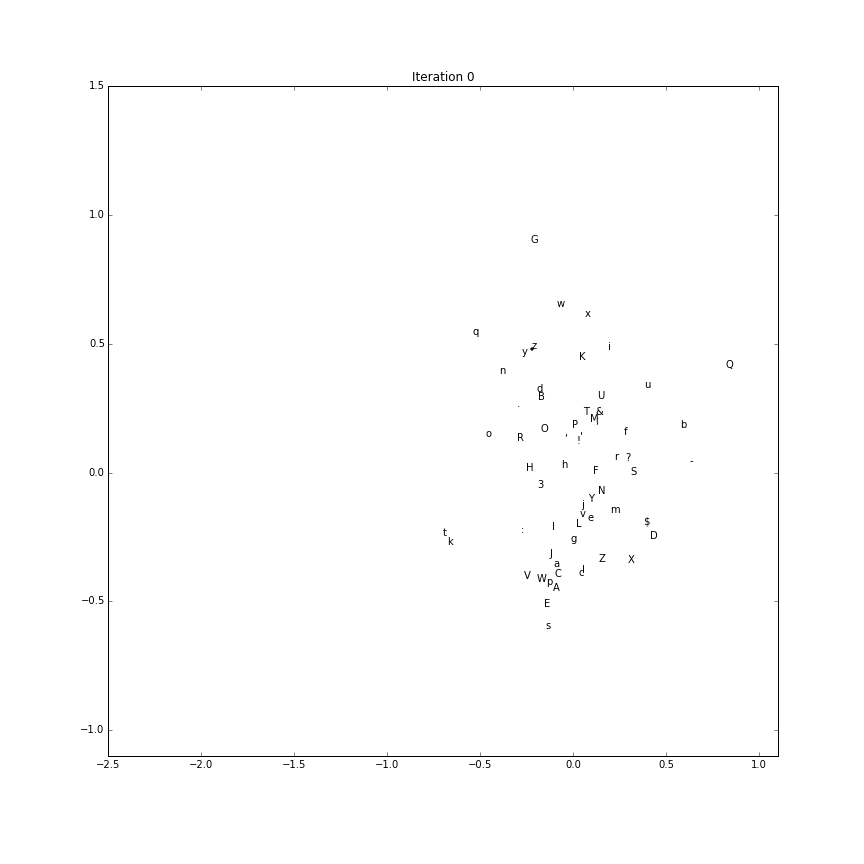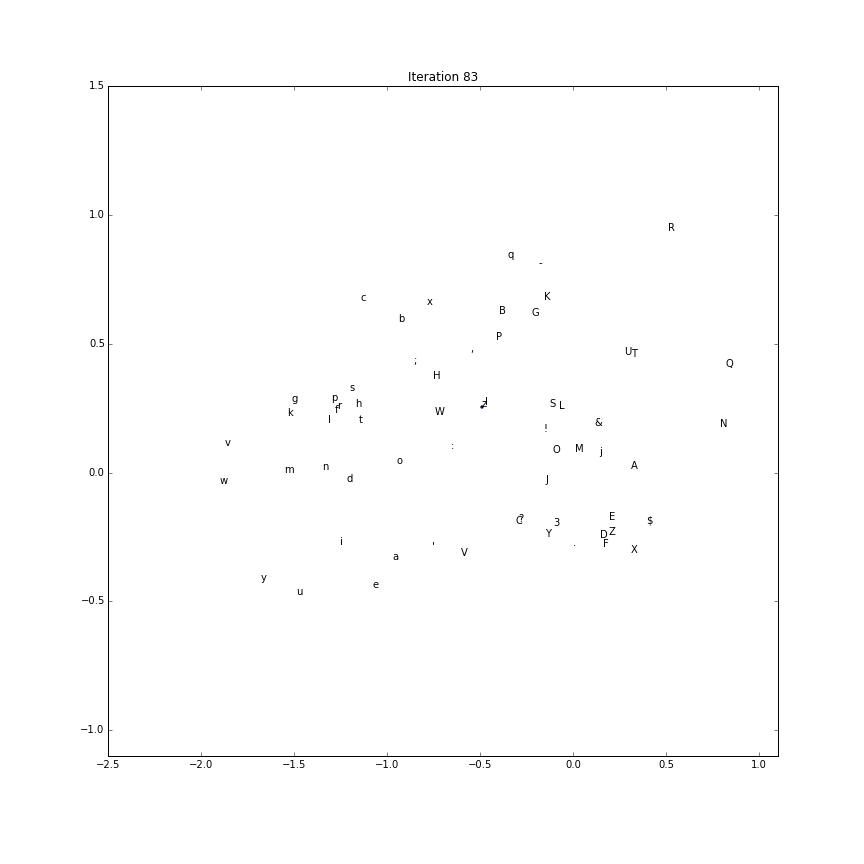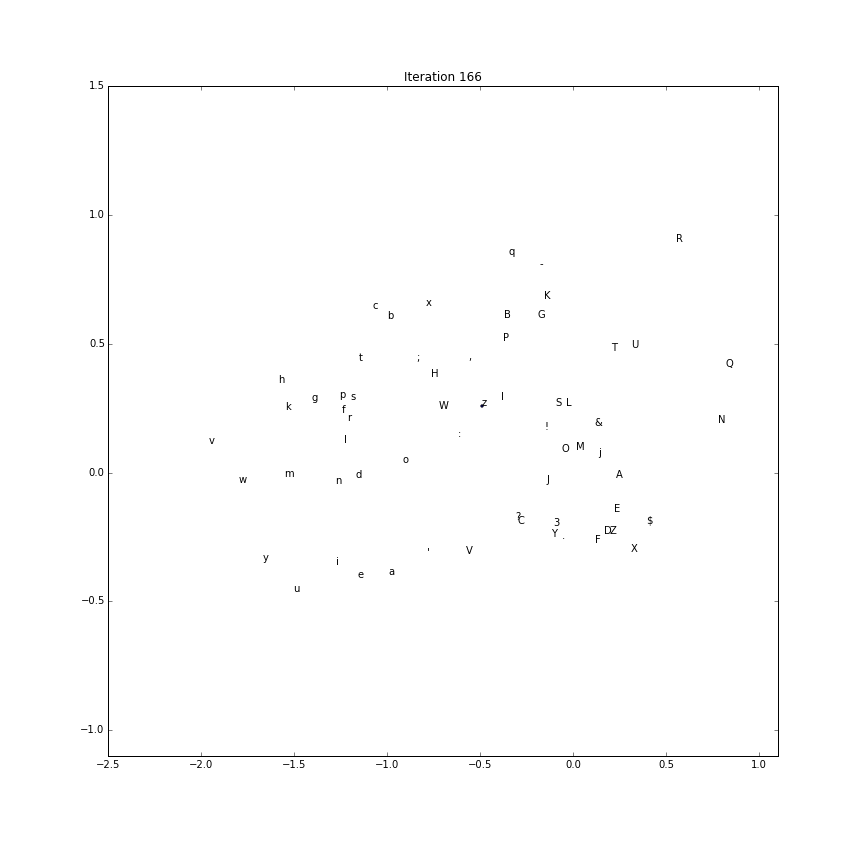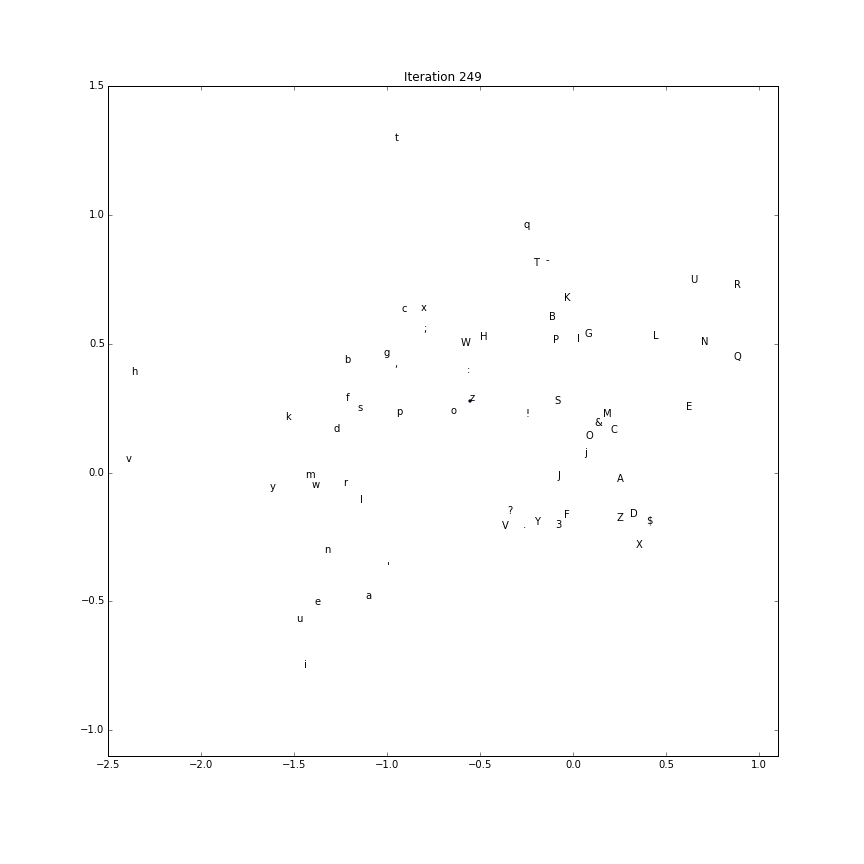
(The first two componenents of each character embedding as training processes:) Embeddings

Generate

This model is expected to work about as well as character N-grams, so let’s generate some text to get a feel for what it does:

def predict_proba(params, M, H, X):
    V = X.shape[1] / M
    N = X.shape[0]
    C = (len(params) - V*H) / (M * H)
    E = params[0: V * H].reshape(V, H)
    W = [params[V * H + c * M * H: V * H + (c + 1) * M * H].reshape(M * H, 1) for c in range(C)]
    R = np.kron(np.eye(M), E)
    
    p = np.zeros((N, C))
    for n, x in enumerate(X):
        logZ = -np.inf
        for c in range(C):
            en = np.dot(np.dot(x, R), W[c])
            logZ = np.logaddexp(logZ, en)
            p[n, c] = en 
        p[n, :] -= logZ
    return np.exp(p)

def generate(params, M, H, n, start):
    V = len(vocab_to_index)
    for i in range(n):
        x = np.zeros((1, M*V))
        for i, c in enumerate(start[-M:]):
            x[0, i*V + vocab_to_index[c]] = 1
        nextchar = vocab[np.random.multinomial(1, predict_proba(params, M, H, x).flatten()).argmax()]
        sys.stdout.write(nextchar)
        start += nextchar

generate(optimizer.theta, M, H, 300, 'The')

The model (which is trained on a small piece of Shakespeare) gives:

e! shye thole,
nsretH torpthe lor.

Towd-pe; yore'n Gprthr toas uount ool I
Anh y and- yaw ancacame.

CUTHURMA:
INROMd?
His:
CNwond.

FLRXDZM&zrele hed varadd bheons;
I law sade piot io her fitponeve py nolr, it ans torl tist,
ar thar hat anasd yoind, feat ye sraps thon-rasg.

S Rosg- folbel, sheron 

Unfortunately the implementation is very slow to train. This means that we are restricted to small N-grams and small embedding dimensions—which means that it’s not going to work very well.

I can try to optimise the implementation to run faster but next I’ll rather try to implement the same model with chainer to show how much simpler and better automatic differentiation makes things.

Written on January 21, 2016